|
I always thought of Anthony Bourdain as a perfect cynic with a solid grasp on things. When he died by suicide, I realized Bourdain was perhaps a depressive cynic with an intermittent grasp. Two Bourdain episodes stick in my mind. When he visited Beirut, we watched from the terrace of his posh hillside hotel while close-support bombers came over the hill behind him and struck downtown Beirut in front of the sea. Tony didn’t get out much that week. When he visited Uruguay, Bourdain hung out awhile at a decrepit beach bar on a shoddy estuary. The bar had a small blind penguin, about the size of cat, that crapped on the floor. Tony had a beer. Bourdain was a fine chef, and I see him as a philosophical medieval manuscript with penis-doodles in the margin. We all grasp as much as we can, and Praxis makes perfect.
0 Comments
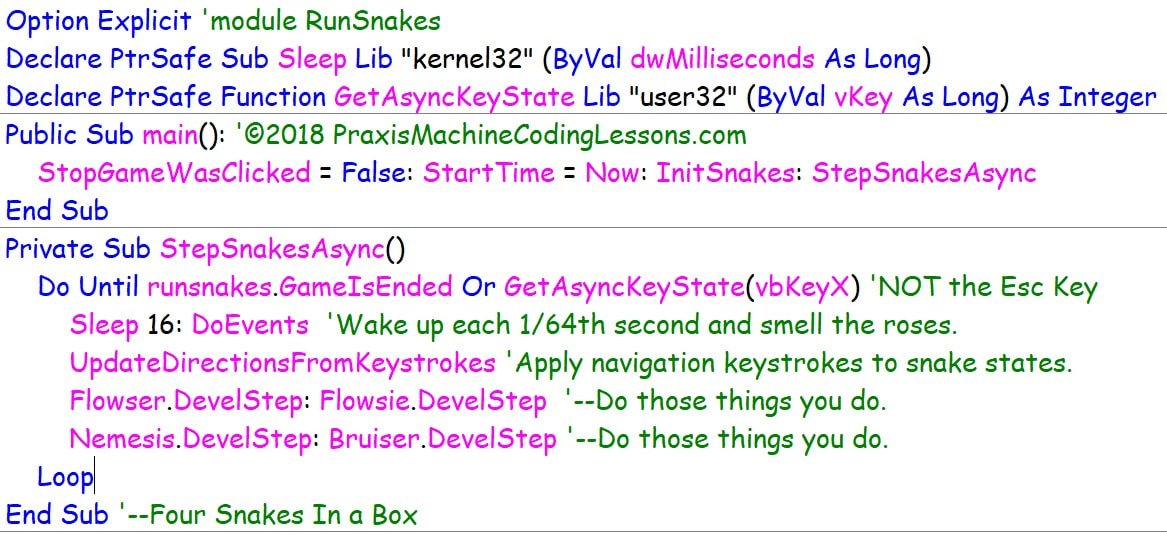
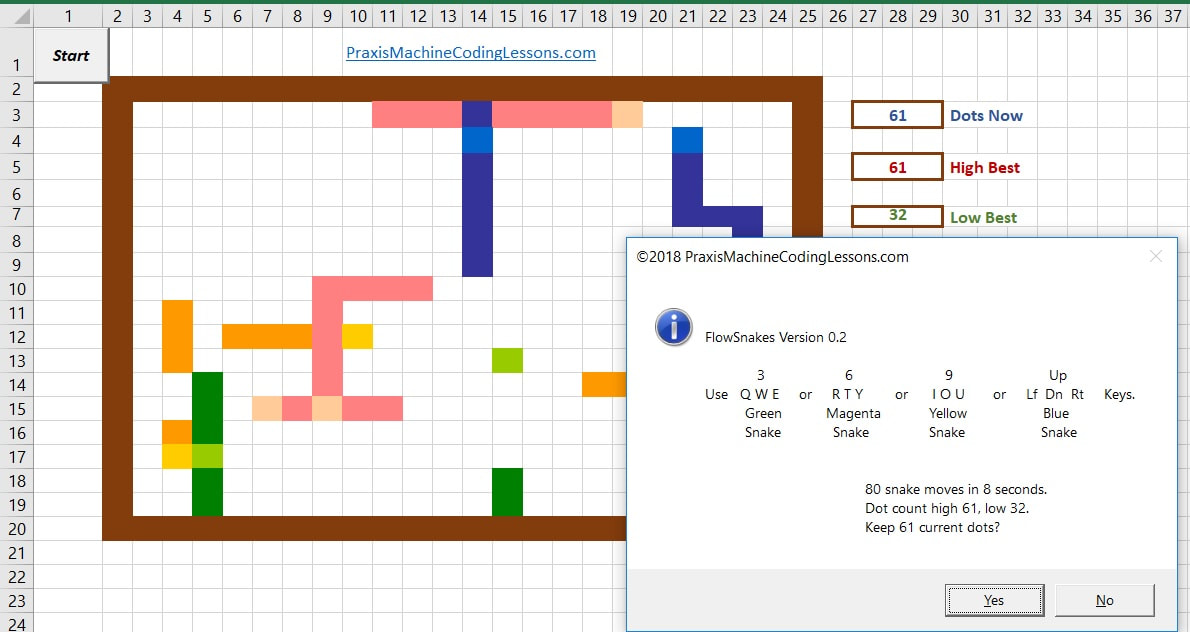
Yes, stimulating sounds weird. But simulating sounds boring. So I wrote FlowSnakes to show how pre-emptive multi-tasking really works—not at the microsecond level, but at the 1/64th second level—closer to the keyboard than to the chip: The snake class has DNA for four kinds of snakes. Flowser and Flowsie are like brother and sister—one blue, one green, same speed, same length. Nemesis is longer and faster—he's out to get Flowser and Flowsie. Bruiser is short and slow—but he can almost walk thru walls. Each snake has his/her own QWERTY controls: The FlowSnake game is in a deliberately undercoded state, and I don't mean Ohio. Just one example, snakes bounce back rather than turn when they hit a wall. Existing FlowSnake code is part of a larger curriculum initiative at www.praxismachinecodinglessons.com/async-excel-snakes.htm When better snakes are built, better high school students will build them, but I digress. Meantime, you are welcome to practice your multi-snake dexterity, review snake class code and initialization routines, propose improved snake behaviors, and critique the pedagogical thrust of FlowSnakes in general.
Also, please let me know if you can break the existing snakes in new and interesting ways.
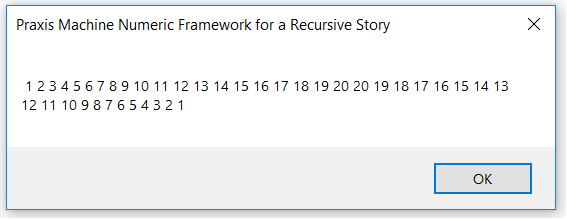
I kept at writing a sleepy-bear program, and I feel a little better now. Here’s what I learned. VBA can only recurse to a maximum depth of about 6,000 or 7,000 calls. Tail recursion and head recursion both max out at the same depth. No optimization for tail recursion takes place. Furthermore, I learned that the sleepy-bear program is a great example of head recursion COMBINED WITH tail recursion. Three phases of recursion take place: first, you deepen the story; second, you report the bottom-level of the story, third you wrap up each previous level of the story. Phase One performs head recursion to push each insomniac animal onto the stack. Phase Two occurs when the stack hits bottom—recursion reaches its pre-determined maximum depth and reports a sleepy animal who buys the story. Phase Three performs tail recursion to unwind the stack; each insomniac sub-story gets a happy ending all the way back up the stack—until the original baby bear finally falls asleep. I built and tested the sleepy-bear idea in stages. First, I made a NON-recursive program consisting of 2 separate, consecutive FOR-NEXT loops that performed the string-handling. My first loop introduced insomniac animals 1 through 4; then I put a 5th animal to sleep between the two loops; then I looped out, putting animals 4 through 1 to sleep. In the second stage, I wrote a heads-and-tails numeric recursion framework that merely counted from 1 to 20 going in and counted back from 20 to 1 coming out: Third, I fleshed out this numeric recursion framework to concatenate boiler-plate narrative text using reasonably cool animal names taken from a hard-coded string array: String concatenation looks naturally stinky, so I recommend reading the simpler numeric recursion subroutine first, to visualize what heads-and-tails recursion actually does. Note that my simple numeric recursive subroutine outputs the final stack value, 20, twice—which does not serve the animal narrative correctly. It’s a worthwhile exercise to fix this numeric recursion framework so that it puts the number 20 to sleep only once! Next consider my claim that VBA recursion maxes out with a stack-overflow error after 6,000 or 7,000 calls. I verified this claim by stress-testing my numeric framework subroutine whilst pushing single integers onto the stack during each recursion. What if I had decided to push the entire “story-so-far” onto the sleepy animal stack? (In reality, I choose to make my text-narrative recursion perform its cumulative work upon a general declaration variable, BedtimeStory, outside the recursion stack.) For sure, a fat string stack would never make it to 6,000 calls! On the other hand, the fat stack would provide its own opportunity to observe and experiment with how much raw stack space VBA is actually willing to allocate. (C# has its own allocation attitudes, but I digress. Don’t even get me started on the charms of the .NET StringBuilder object) In summary, I think creating a deliberately string-clogged VBA stack is a worthwhile exercise—up to a point. Deliberate stack-clogging is a way to make recursion feel physical, not just logical. After all this, do I like recursion better now than I used to? Well yes, but only a little.
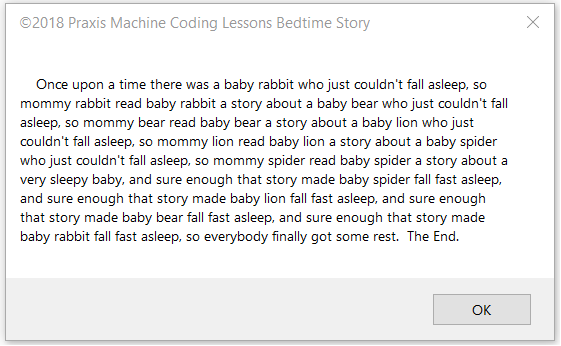
I’ve thought of a great way to manage my aversion to recursion. I’m going to write a simple and cute NON-recursive program to generate the insomniac bunny story—you know, “Once upon a time there was a Baby bunny who just couldn’t fall asleep, so Mommy rabbit read Baby bunny a story about a Baby bear who just couldn’t fall asleep so Mommy bear read the Baby bear a story about …,” and so on until you finally encounter a story in which a baby animal falls fast asleep, and sure enough the stack unwinds, and Mommy rabbit finally gets some sleep. THEN I will write a recursive program about a programmer who just couldn’t bring himself to deal with recursion, so he wrote a program about a programmer who—Oh, never mind, I need to get some sleep first.
It’s been a long and lovely day. If you seek to introduce computer science into a liberal arts high school mathematics curriculum, then Chris Bishop is your man. He’s Professor of Computer Science at University of Edinburgh, and Laboratory Director of Microsoft Research in Cambridge England. In the forward to John McCormick’s 9 Algorithms that Changed the Future (Princeton University Press 2012,) this is what he said. This is what Chris Bishop said:
“One reason for the relative lack of appreciation of computer science as a discipline is that it is rarely taught in high school. While an introduction to subjects such as physics and chemistry is generally considered mandatory, it is often only at the college or university level that computer science can be studied in its own right. Furthermore, what is often taught in schools as ‘computing’ or ‘ICT’ (information and communication technology) is generally little more that skills training is the use of software packages. Unsurprisingly, pupils find this tedious, and their natural enthusiasm for the use of computer technology in entertainment and communication is tempered by the impression that the creation of such technology is lacking in intellectual depth. These issues are thought to be at the heart of the 50 percent decline in the number of students studying computer science at university over the last decade. In light of the crucial importance of digital technology to modern society, there has never been a more important time to engage our population with the fascination of computer science.” Really, there’s nothing more I can say. But there’s plenty more to be done…. My goal here is to describe 6 or 8 one-semester computer electives in high school mathematics leading up to and/or beyond AP Java and AP Computer Science, plus a semester course on Book One of Euclid’s Elements explaining how ancient Greek concepts of the objects and methods of mathematics are relevant to school mathematics today.
Let me get my thoughts on Euclid off my chest first. Euclid of Alexandria drew his concepts of mathematical points and lines in a plane from outside mathematics, namely from mechanics, specifically from two simple idealized mechanical tools—the floppy compass and the unmarked straightedge. Floppy and unmarked meant that Euclid’s derivation of geometry was coordinate-free, that is, not based on numeric transforms preserving shape and/or area. Likewise, Alan Turing drew his concept of arithmetic computability from outside number theory and formal logic, namely from local manipulation of strictly adjacent symbols using pencil and eraser on an idealized endless tape. It’s amazing to me that Euclid and Turning revolutionized mathematical explanations and insights along the same lines—by moving away from the big picture and concentrating on localized procedures. For both men, the pen was not mightier than the sword. Rather, the eraser was mightier than the pencil! Talk about less is more! I love it when a curricular purpose comes together. You can see my Day-One 9th Grade lesson introducing the MessageBox at PraxisMachineCodingLessons.com, under Lessons for Students. Now I want to take a first cut at the whole picture. All my courses from the very first intend that students can operate with mathematical tools consciously, not just correctly. Self-awareness concerning mathematical activity, symbols and tools is the core of my curriculum. Euclid and Turing were both aiming at mathematical self-awareness, and my students must develop an instinctive sense of “Simon-Says-May-I” where mathematical gestures are concerned. To be frank, this self-analytic mindset does not sound like a middle-school mindset to me. Therefore I don’t want my curriculum pushed down below 9th grade—not even for the hopelessly precocious. I admit that self-analytic mathematics doesn’t exactly sound like typical 9th thinking either, but at least high schoolers are more in the ballpark. At least they modulate a hundred times a day between painful self-awareness and total cluelessness. And their math thinking is no exception. For me, self-analytic mathematics ‘merely’ requires Piaget’s highest level of mental processing, namely, formal operational thinking. Piaget observed that formal operational thinking comes online in adolescence and continues throughout adulthood, but ‘continues’ is too strong a word. In reality, all of us grownups engage in formal operational thinking only sporadically—typically when all else fails, and often not even then. Instead, most of us grownups happily accept semi-permanent self-contradictory premises in our thinking, especially in areas we care about strongly. So let’s not impose additional mental self-awareness upon our young middle school citizens during the early throes of adolescence. Instead, let’s warm up our middle schoolers for formal computer science thinking via plenty of concrete operational technology—tools and tasks such as robotics programming, 3D printing, systematic data gathering, spreadsheet calculations, and so forth. We’ll reserve ‘real’ formal computer programming for the high school curriculum. But how much can we reasonably expect in the way of abstract mathematical thinking from a general high school mathematics population starting in 9th grade? To be sure, we’re proposing an elective computer curriculum and students with ‘the knack’ will self-select themselves. But it would be very nice if a significant fraction of all freshman and sophomores selected a half-credit or more of ‘real computer programming’ alongside their core mathematics required for graduation. After all, programming computers is at least as cool and provocative as dance, psychology, or business management. And formal computer thinking could actually energize and fertilize mathematical thinking in required algebra and geometry courses taken alongside. Guidance counselors could think of computer programming courses as non-remedial math intervention. So here is our dilemma: how can we foster success, accountability and graduation credit in mathematics for all high school students who elect computer programming, particularly students who opt into beginning computer programming courses with no intention of going “all the way”? Can we offer them a middle ground between easy-A and geeks-only? Supporting the ‘easy’ side is the fact that computer programming is inherently hands-on with lots of instant feedback. Pressing the keys and moving the mouse is bound to produce some results, and teacher’s brief suggestions can often demolish roadblocks to intended results. Supporting the ‘geek’-side is the fact that computer programming is indeed something you have to do, not just talk about or appreciate. Computer programming is a form of technical writing and editing, and every computer language really is a language all its own. But a first-semester high school computer programming course should be a fun-run, a come-one-come-all footrace for a good cause. Everyone who buys the sweatshirt receives the recognition provided they actually start the race and finish at least half the course. A good time will be had by all, provided you can arrange things so that the sprinters and the stragglers do not get in each other’s way. I have in mind a modified mastery grading system—mastery of the first 60% of the course for a grade of D, 70% for a C, and so forth. The hands-on nature of computer thinking and coding makes individuated progress in the second half of the semester more practicable than you might think. The first half of each semester would be primarily group-oriented, lecture-based, and hands-on every day. The second half of each semester would be primarily project-oriented, tutoring-based, remedial as necessary, and hands-on every day. Course Breakdowns Will Follow …. Casting About For an Elective High School Curriculum in Computer ProgrammingIt has always struck me as odd that the high school mathematics curriculum has three years of algebra, geometry, and trig courses leading up to AP Calculus, but there is no established curriculum leading up to AP Java or the newer AP Computer Science Introduction. Perhaps that’s why these AP computer courses are oddly introductory despite their Advanced Placement college status. I mean, high schools seniors who seriously ace BC Calculus are truly launched towards a college math degree. But high schoolers who ace AP Java and Computer Science are still on the tourist bus towards a professional degree in computing.
Admittedly, there’s only so much you can accomplish in an introduction from scratch. And the AP computer curriculum is still relatively new. By contrast, the traditional four years of high school preparation for calculus is now almost two centuries old. Harvard first required a high school Algebra background for all entrants in 1829. To this day, four years of mainstream high school mathematics articulates well with the first two years of a math major in college. But the world of electronic digital programming is much less than 100 years old, and the dust is far from settled on its standard curriculum. Two instructional highpoints stand out. Back at the dawn of deeper-higher computing languages, Kernighan and Ritchie first presented “Hello World” in C in 1978. Back at the dawn of human consciousness of computers, Alan Turing first presented a mathematical description of computability and computational undecidability in 1936—now that was a singularity! Today’s high school computer curricula (and college computer curricula, for that matter) are still struggling to get their boots on the ground. Pedagogical things like this take time. More than decades, for sure. Several centuries of ancient Greek mathematics preceded Euclid’s teachable presentation of it. But right now is not too soon (and it’s certainly not too late) to institute a four-year high school computer curriculum (elective, of course) that honors the roots and branches of computer science and the coding arts as they exist today—still within living memory of their origins. Calculus after Descartes and Newton took three centuries to achieve a well-settled curriculum. During those centuries, calculus quietly transformed physical science, but calculus did not begin to transform our physical world until the 20th century. That’s when calculus first became an indispensable engineering tool for everything from radio and television to space rockets and exploding atoms. On the other hand, computer science shot right into the fabric of our present highly engineered human condition while formal computational programming concepts and semi-conductor logic circuits were still both in their infancy—or their adolescence at best. Hardly has there been enough time to discern where we are with computers, let alone how we got here. Certainly there’s not been enough time to organize a settled curriculum for initiating young people into the wonders of formal machine computing. Disciplines such as literature, history, even welding have well-settled high school and college curricula by comparison. No surprise that Doonesbury, who clearly has a fix on our present computer-based human situation, works in a cubicle not a classroom. So it’s not too sad that adequate high school curricula in computer coding and digital systems are mostly lacking today. Rather today is the right time to start teaching the right stuff in high school: procedural algorithms, hierarchical processing structures, stateful objects, architecture of computing machines, distributed networks, relational databases, query languages, markup languages—all the good stuff—suffused with the living history and philosophy of formal computing. Too ambitious? Not at all! In fact, it’s already been tried a little. Look around for a full four-year high school computer curriculum that starts 9th grade with Kernighan & Ritchie’s iconic program, “Hello World.” The first and best such curriculum you’ll find is at codehs.com, and it’s even in Java! Hey students! Click the Colorful Primes to see facts about computing the first million primes.
Hey Teachers! Click the Turing Tape below to visit PraxisMachineCodingLessons.com.
|
Capt. PeteWhen Peter is on land, he develops curricula for teaching Computer Science to all high school students via coding elementary apps in multiple professional development environments. Archives
December 2017
Categories |
||||||||||||